
In the project Slow feature Analysis: Unsupervised learning of invariances I have shown that the slowness principle can be used to learn translation and other invariances for whole objects in a hierarchical network model. However, the retina was only one-dimensional and the stimuli were very artificial. In this project we wanted to move to more natural stimuli, but for simplicity we first considered only one layer rather than a whole hierarchical network. Thus we applied slow feature analysis (SFA) to quasi-natural image sequences (derived from static natural images) and obtained units that were (inhomogeneous) quadratic forms (functions). We compared these with complex cells in primary visual cortex of primates and found that they have many properties in common.
Obtaining the results was fairly straightforward and a matter of weeks, really. Analyzing the units (quadratic forms) we had gotten and comparing them with physiological results was the hard part. For the analysis we have partly used traditional methods known from experiments and partly have developed new methods, see the project Analysis of inhomogeneous quadratic forms as receptive fields. The units we have obtained
- have optimal stimuli that look like Gabor wavelets,
- are insensitive to the phase of the wavelets,
- have a similar set of orientation tuning curves as complex cells, see Figure 1,
- show sometimes end- and side-inhibition, see Figure 2, and
- are sometimes direction selective, see Figure 1.
Thus, our units are remarkably similar to complex cells in primary visual cortex. What we don't get is much of a localization of the receptive fields. They usually cover the whole image patch we are simulating.
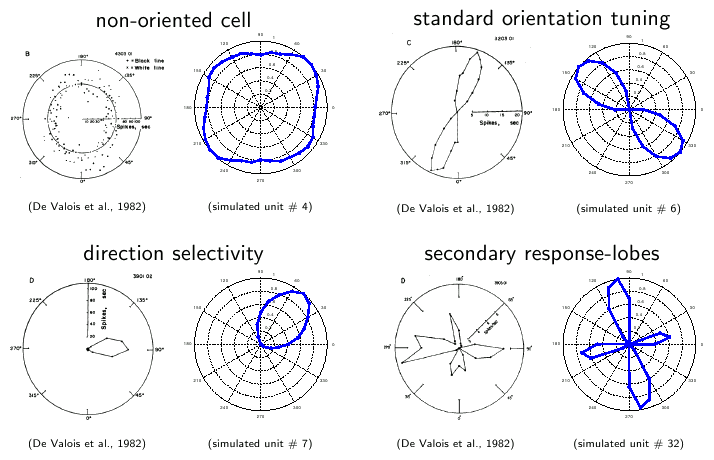
Figure 1: Orientation tuning curves of complex cells (left, black lines) and SFA units (right, blue lines) in comparison. The response of the cells/units is plotted in radial direction as a function of the orientation of a grating shown to the cell/unit. Drifting gratings were used and responses 180° apart come from the same grating orientation but different drifting direction. Thus, the cell/unit at the bottom left is direction selective while the others are not.
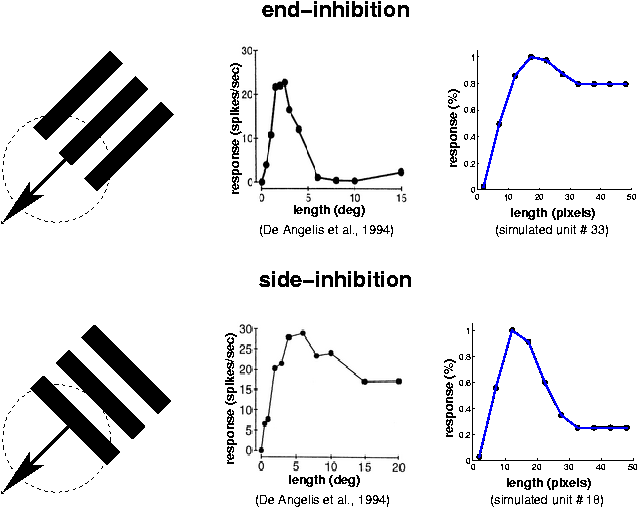
Figure 2: As one moves a grating into a receptive field of a complex cell (left) the response typically increases. There are some cells where the response starts to decrease again at some point (middle). Such cells are called end- or side-inhibited, depending on the orientation of the grating relative to the direction of movement. Some of our SFA units show exactly that same bahavior (right). The level to which the response dropes varies greatly within each class of cells/units so that the differences seen here are not significant.
Interestingly, the results that we get do not depend on the higher-order statistics of the images. We get virtually identical results if we start with colored noise images. What matters are the transformations that we apply to the static images to generate the image sequences. The most important one is translation.
See also the project page "Slowness as a computational principle for the visual cortex" by Pietro Berkes, which includes Matlab code for performing the simulations of this project. Python source code for SFA and several other learning algorithms written by Pietro Berkes and Tiziano Zito is available at http://mdp-toolkit.sourceforge.net/.
