
In theoretical as well as experimental studies receptive fields are often formalized as linear or (inhomogeneous) quadratic forms (functions). While the interpretation and visualization of a linear receptive field is trivial and straightforward, it gets more complicated for quadratic forms. In context of our project on the selforganization of receptive fields with SFA we have developed different methods of visualizing the functional properties of a quadratic form. Two of them are particularly useful and generally applicable, namely those yielding the optimal stimuli and the invariances.
Given a quadratic Form
where x is the input image written as a vector and y is the output activity of the unit, while H is a square matrix, f is a vector, and c is a scalar. If y(x) is supposed to represent a receptive field, the first question one might ask is "What is the optimal stimulus that drives this unit best?". To make this question meaningful, one has to constrain x somehow, because otherwise one could generate arbitrarily high output activities by simply making x large enough (if x points in a direction where the quadratic term has a positive value). If we constrain the norm of x to a certain value that is typical for the input stimuli, the optimal excitatory stimulus with that norm can be calculated. For the quadratic forms resulting from applying SFA to image sequences we get optimal stimuli that look like Gabor wavelets (Fig. 1), which is in nice agreement with physiological results for complex cells in primary visual cortex. One can similarly calculate the optimal inhibitory stimuli, which in our case also look like Gabor wavelets (not shown).

Figure 1: Optimal stimuli of quadratic forms that were selforganized by applying SFA to quasi-natural image sequences. Six out of hundred units ordered by slowness (slowest first) are shown.
The optimal stimulus only gives partial information about the quadratic form. The next question one might ask is "How can I vary the optimal stimulus such that the output decreases as little as possible?", which is the question of invariances. Again the norm of x must be fixed to the set value. A single unit usually has several (almost) invariant directions. Interestingly these directions can often be interpreted quite nicely. Animation 1 shows the first five invariances of unit # 14.
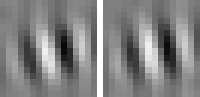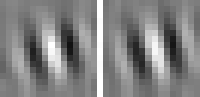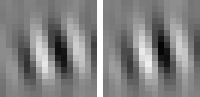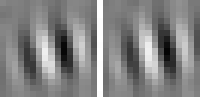
rotation invariance
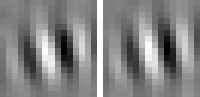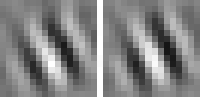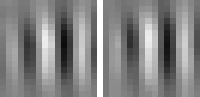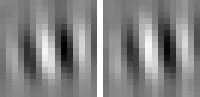
shift invariance
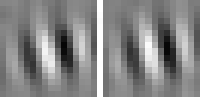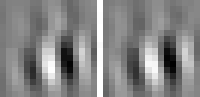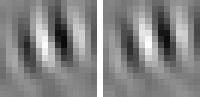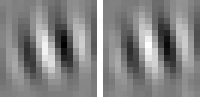
curvature invariance
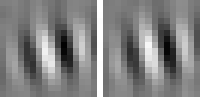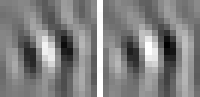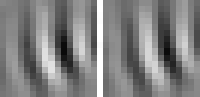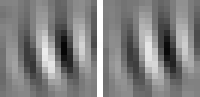
size invariance
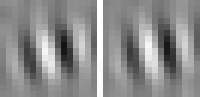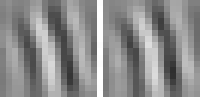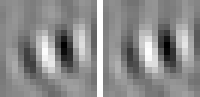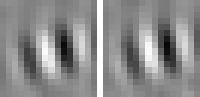
Animation 1: First five invariances of unit # 14. They can be interpreted as phase, rotation, shift, curvature, and size invariance.
We have also considered other ways of visualizing quadratic forms, such as Volterra-kernels and eigenvectors of matrix H and discuss the pro and cons.
See also the project page "On the analysis and interpretation of inhomogeneous quadratic forms as receptive fields" by Pietro Berkes, which includes Matlab code for the methods we have developed.
