For visualization purposes and for applying transformations to an image after it has been transformed by a set of linear filters, it is important to be able to reconstruct the image from transformed data faithfully. Reconstruction is trivial if the filters are orthogonal. For affine sets of filters, such as the Gabor wavelets, an orthogonalization procedure needs to be employed a posteriori. We have developed a method that can also be applied to a sparse subset of transformed data as required for labeled graphs.

Figure 1: Different reconstruction methods for one location. First column: Original images with the central pixel marked by a cross. Second column: Reconstructions from the full Gabor wavelet transform, i.e. at all pixel positions. Third column: Reconstructions from one jet, i.e. the Gabor wavelet transform at the central pixel only. Last column: Reconstructions from one jet if the affine properties of the Gabor transform are not taken into account, i.e. if it is done the naive way.

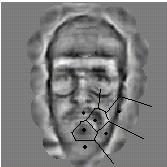
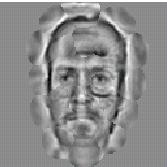
Figure 2: Reconstruction methods for a graph. Left: A face with a graph, which is labeled with Gabor jets. Middle: A reconstruction of the image from the graph. Right: A reconstruction of the image from a face bunch graph, i.e. no information from the original image has been used but only the best fitting jets of a set of 100 other faces.

