For the Impatient
What is BBComp?
BBComp — the black box optimization competition — is the
first competition in continuous black-box optimization where test
problems are truly black boxes for participants. It is also the first
web/online optimization competition in the direct search domain.
News
September 16, 2019. As promised already for a long, long time, we have now finally published the code for evaluating the objective functions used in our competitions. It is available from the downloads section. The code is published in the hope that it will be useful, in particular for the evaluation and comparison of optimization algorithms.
Background
"Black Box" optimization refers to a problem setup in which an optimization algorithm is supposed to optimize (e.g., minimize) an objective function through a so-called black-box interface: the algorithm may query the value f(x) for a point x, but it does not obtain gradient information, and in particular it cannot make any assumptions on the analytic form of f (e.g., being linear or quadratic). We think of such an objective function as being wrapped in a black-box. The goal of optimization is to find an as good as possible value f(x) within a predefined time, often defined by the number of available queries to the black box. Problems of this type regularly appear in practice, e.g., when optimizing parameters of a model that is either in fact hidden in a black box (e.g., a third party software library) or just too complex to be modeled explicitly.
If you are wondering about the No Free Lunch Theorem in this context then please read the FAQ.
A large variety of optimization algorithms for continuous black box optimization has been proposed. The power of these algorithm is usually assessed on collections of benchmark problems. This is an important approach to comparability of scientific results. However, it means that the problem to be optimized is known to the experimenter, and hence it is not truly a black box.
Goals and Scope
The black box optimization competition aims to close this gap by providing an algorithm testbed that is truly a black box to participants. Our testbed consists of a wide range of benchmark problems. The only information known to the optimizer is the dimension of the problem, bounds on all variables, and a budget of black box queries.
In this competition – just like in the real wold – there is no second chance! You do not get to try a second method if you fail. However, you are of course free to use your budget in any way, which includes the possibility of reserving a certain fraction of the budget for algorithm selection and parameter tuning. We also regard the optimization procedure as a black box; feel free to do whatever you think works best in a proper black box optimization setting.
The competition goals differ from those of established testbeds for black box optimization algorithms (see the related material). We do not take the perspective of comparing algorithms. Such a comparison will come out as a side effect in the end. However, this would mean that each participant could throw a large number of entries into the ring and see which performs best. Here we allow for only a single entry per participant. This shifts the focus from a comparison of algorithms to a competition of participants.
How to Participate
We provide software for evaluating black box functions from a predefined set of benchmark problems. The software makes sure that the predefined budget of evaluations is not exceeded.
Interfacing this software is easy. Example code is provided for C/C++, Java, Python and Matlab. We strongly recommend to rtfm.
The software requires an internet connection with access to the competition server (this very machine that also delivered this web page to your browser). Moreover a personalized account is required, which can be requested by writing an email with you affiliation and your preferred user name to blackboxcompetition@gmail.com. The account is needed for the competition, but software can be tested beforehand without creating an account.
In the spirit of open and reproducible research the organizers appreciate if participants provide their optimization software, e.g., as open source. However, this is no prerequisite for participation! Closed-source algorithms are explicitly allowed. Participants do no need to submit or publish their optimization software or its source code. In the 2015 and 2016 organized within the CEC and GECCO conferences, participants do not need to write a paper.
It is possible to participate anonymously in the competition. There is a "public name" field in the account data. Participants may enter their real name (or research group, as appropriate), but they are also free to enter a pseudonym. Only the public name and the method short description (if any) will be published together with the results after the end of the competition.
Competition Rules
The rules are simple. For each of the problems defined in a competition track, each participant can use any optimization method (including manual and interactive methods) to find a point x with as good as possible value f(x) within a predefined budget of black box queries. The queries are to be conducted through the binary dynamic library found in the downloads section.
It is against the rules of the competition to disassemble or otherwise reverse engineer the provided binary software libraries and to intercept or modify their network connections. It is against the rules to gain access to the competition server – this is even against the law.
Note: Each participant has only one single attempt. Please make double sure that your software works correctly before starting the actual competition runs. We provide "trial" tracks for software testing and debugging.
Evaluation criteria
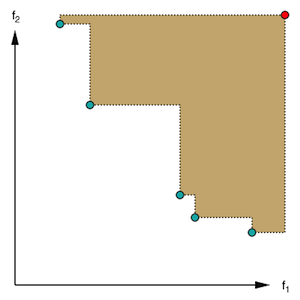
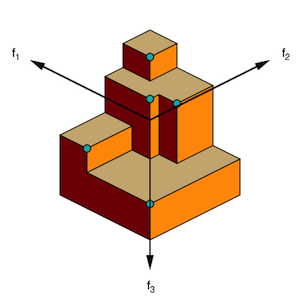
Performance Definition We unify the evaluation of single-objective and multi-objective optimization problems by first defining a notion of performance. The goal of all single-objective problems is to find an as small as possible function value within the given budget. Hence the performance measure is the smallest function value. For multi-objective optimization the goal is to dominate as much of the objective space as possible, where all objectives are to be minimized. Hence performance is measured by the dominated hypervolume, which must be maximized. To stay compatible with the minimization perspective of the single-objective case, we define multi-objective performance as 1 - HV, where HV is the dominated hypervolume (for multi-objective optimization all objective values are guaranteed to be in the unit interval, and we chose the vector of all ones as the reference point for the computation of the hypervolume). The above definition yields a performance value for each participant on each problem.
Overall Ranking The aggregation of performance over all problems in a track is analog to the formula one scoring system. In this analogy each participant corresponds to a driver and each benchmark problem of the competition track corresponds to a race track. For each problem participants are sorted w.r.t. performance and the top scorers receive points depending on their rank. The sum of these points over all problems is the overall score. Participants are ranked w.r.t. this overall score.
Tie Breaking For some (rather easy) problems we expect multiple participants to achieve near-optimal and hence extremely close results. In this situation purely numerical differences–possibly even depending on programming language and compiler–can decide upon the lion's share of the points (distributed among the top ranks). Hence the ranking procedure is slightly modified as follows: Let ƒ* denote the best overall performance achieved for a problem. Based on this value a numerical imprecision range is defined as ε = max(10-14 • ƒ*, 10-20). All algorithms with performance values better than ƒ* + ε share the first rank, while all worse algorithms are ranked according to their exact performance.
Alternative assessment procedures will be considered as well, however, their results will not affect the selection of the winners.
Problem Statistics
This section summarizes properties of the optimization problems in different tracks. The values are for reference, the same information can be obtained from the software interface.
| track name | dimensions / number of objectives | problems per dimension | total number of problems | budget |
|---|---|---|---|---|
| trial | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 | 100 | 1000 | 100 dim2 |
| trialMO | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 / 2, 3 | 50 | 1000 | 1000 dim |
| BBComp2015CEC | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 | 100 | 1000 | 100 dim2 |
| BBComp2015GECCO | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 | 100 | 1000 | 10 dim – 100 dim |
| BBComp2016-1OBJ | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 | 100 | 1000 | 100 dim2 |
| BBComp2016-1OBJ-expensive | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 | 100 | 1000 | 10 dim – 100 dim |
| BBComp2016-2OBJ | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 / 2 | 100 | 1000 | 1000 dim |
| BBComp2016-2OBJ-expensive | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 / 2 | 100 | 1000 | 10 dim – 100 dim |
| BBComp2016-3OBJ | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 / 3 | 100 | 1000 | 1000 dim |
| BBComp2017-1OBJ | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 | 100 | 1000 | 100 dim2 |
| BBComp2017-1OBJ-expensive | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 | 100 | 1000 | 10 dim – 100 dim |
| BBComp2017-2OBJ | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 / 2 | 100 | 1000 | 1000 dim |
| BBComp2017-2OBJ-expensive | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 / 2 | 100 | 1000 | 10 dim – 100 dim |
| BBComp2017-3OBJ | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 / 3 | 100 | 1000 | 1000 dim |
| BBComp2018-1OBJ | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 | 100 | 1000 | 100 dim2 |
| BBComp2018-1OBJ-expensive | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 | 100 | 1000 | 10 dim – 100 dim |
| BBComp2018-2OBJ | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 / 2 | 100 | 1000 | 1000 dim |
| BBComp2018-2OBJ-expensive | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 / 2 | 100 | 1000 | 10 dim – 100 dim |
| BBComp2018-3OBJ | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 / 3 | 100 | 1000 | 1000 dim |
| BBComp2019-1OBJ | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 | 100 | 1000 | 100 dim2 |
| BBComp2019-1OBJ-expensive | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 | 100 | 1000 | 10 dim – 100 dim |
| BBComp2019-2OBJ | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 / 2 | 100 | 1000 | 1000 dim |
| BBComp2019-2OBJ-expensive | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 / 2 | 100 | 1000 | 10 dim – 100 dim |
| BBComp2019-3OBJ | 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 / 3 | 100 | 1000 | 1000 dim |
All functions are deterministic (noise free). Querying a point twice yields the exact same function value.
EMO'2017 Real-World Problems
The EMO'2017 track (BBComp2017EMO) consists of 10 challenging real-world problems from various domains, listed below. We thank Michael Emmerich for co-chairing this track. The deadline for the track is at midnight UCT on March 14/15, 2017.
| problem index | problem name | dimensions | number of objectives | budget |
|---|---|---|---|---|
| 0 | welded beam | 4 | 2 | 100 |
| 1 | kernel ridge regression | 5 | 2 | 100 |
| 2 | brake | 4 | 2 | 100 |
| 3 | facility placement | 20 | 2 | 1000 |
| 4 | hydro-dynamics | 6 | 2 | 1000 |
| 5 | heat exchanger | 16 | 2 | 500 |
| 6 | neural network controller | 24 | 2 | 2000 |
| 7 | optical filter | 11 | 2 | 200 |
| 8 | area under curve | 10 | 2 | 500 |
| 9 | vibrating platform | 5 | 2 | 200 |
The problem names reflect the underlying problems without giving any details. Beyond the provided problem names, no further information on the problems or their encoding will be provided before the end of the EMO'2017 competition, in order to maintain the black-box character of the competition. We plan to publish the problems after the deadline.
Downloads
We provide software packages for Windows, Linux, and MacOS for download. The core of each of these packages is a dynamic library. This library acts as the black box.
The dynamic library can be accessed directly from C and from C++. For convenience we also provide pre-built interfaces for Matlab, Python, and Java. We appreciate contributions for further programming languages.
The BBComp client software comes with the following license. The current version of the software is 1.3.1.
Objective functionsCore of the BBComp function evaluator, together with problems and track definitions accumulated over five years. | bbcomp-core-source-gplv3.zip |
Real-world ProblemsSource code of the real-world problems used in the corresponding EMO'2017 track. | realworld-problems-bbcomp-EMO-2017.zip |
Windows 64bitBlack Box competition module for Windows.NOTE: Windows 7 users may have to install version 14 of the MSVC runtime libraries, see e.g. this post. | bbcomp-windows-64bit.zip |
Linux 64bitBlack Box competition module for Unix/Linux. The software has been tested on Linux Mint. | bbcomp-linux-64bit.zip |
MacOSBlack Box competition module for Mac OS X. The software has been tested on Mac OS X Mavericks (10.9.5). | bbcomp-mac.zip |
Bindings for the library have been created in several languages and are freely available – thanks for sharing!
- An R language client by Andrzej Fiedukowicz is available at https://github.com/fiedukow/RBBComp.
- A LUCK language client by Andrew Johnson is available at http://luck.subarctic.org/example/bbcomp.
Results
Summary of the results of the GECCO'2019 competition:
- GECCO 2019 single-objective track
- GECCO 2019 expensive single-objective track
- GECCO 2019 two-objective track
- GECCO 2019 expensive two-objective track
- GECCO 2019 three-objective track
- GECCO 2018 single-objective track
- GECCO 2018 expensive single-objective track
- GECCO 2018 two-objective track
- GECCO 2018 expensive two-objective track
- GECCO 2018 three-objective track
- GECCO 2017 single-objective track
- GECCO 2017 expensive single-objective track
- GECCO 2017 two-objective track
- GECCO 2017 expensive two-objective track
- GECCO 2017 three-objective track
- EMO 2017 real-world problems track
- GECCO 2016 single-objective track
- GECCO 2016 expensive single-objective track
- GECCO 2016 two-objective track
- GECCO 2016 expensive two-objective track
- GECCO 2016 three-objective track
- CEC 2015 track
- GECCO 2015 track
Documentation
Detailed documentation is available on a separate page.
Frequently Asked Questions
The FAQ is found on a separate page.
Related Material
We would like to provide links to related material on black box optimization benchmarking and corresponding conferences:
- GECCO'2017
- Black-Box Optimization Benchmarking (BBOB) 2016, including multi-objective optimization for the first time
- GECCO'2016
- Black-Box Optimization Benchmarking at CEC'2015 (CEC-BBOB)
- CEC'2015 Special Session / Competition on Real Parameter Single Objective Optimization
- CEC'2015 Competition on Large Scale Global Optimization
- CEC'2015
- GECCO'2015
About
The black box competition is organized by Ilya Loshchilov and Tobias Glasmachers. They hold the copyright on all material provided on this website. The material is licensed for the purpose of participation in the competition.
Feedback
We are eager to receive feedback from participants. Don't hesitate to ask questions, propose features, report bugs, start discussions, and share your thoughts and opinions. Write to blackboxcompetition@gmail.com.
Sponsors
We would like to thank Microsoft Research – Inria joint centre for sponsoring the GECCO'2015 track, more specifically, Youssef Hamadi and Laurent Massoulie for their interest and support.
Acknowledgements
We would like to thank Giovanni Iacca for valuable discussions.
