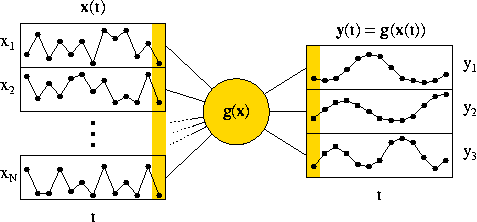
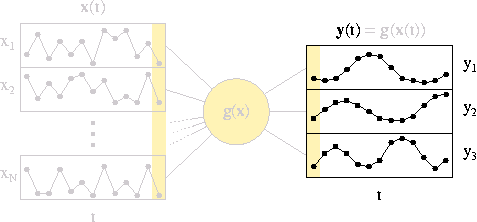
Slow feature analysis (SFA) finds a vectorial input-output function g(x) for a given vectorial input signal x(t) such that the output signal y(t)=g(x(t)) changes most slowly; see Figure 1, left. To avoid the trivial constant response y(t)=const, the components of y are constrained to have zero mean and unit variance and be mutually uncorrelated. This full optimization problem is difficult to treat analytically. I have thus considered a simplified optimization problem, in which the input signal as well as the input-output function are ignored; see Figure 1, right. The question then becomes: What is the optimal free output signal that can be produced at all, regardless of the input but possibly under some general constraints, such as cyclic boundary conditions? An algebraic analysis of this simplified optimization problem provides a fairly detailed understanding of the simulation results obtained in the major experiments of the project Slow Feature Analysis: Unsupervised Learning of Invariances; see Figure 2.


Figure 1, left (or top): Illustration of the optimization problem solved by SFA. The input signal x(t) varies quickly while the output signal y(t)=g(x(t)) should vary slowly. SFA finds the optimal input-output function g(x). Right (or bottom): The simplified optimization problem, which can be analyzed more easily, ignores input signal as well as input-output function. Only the output signal is considered.
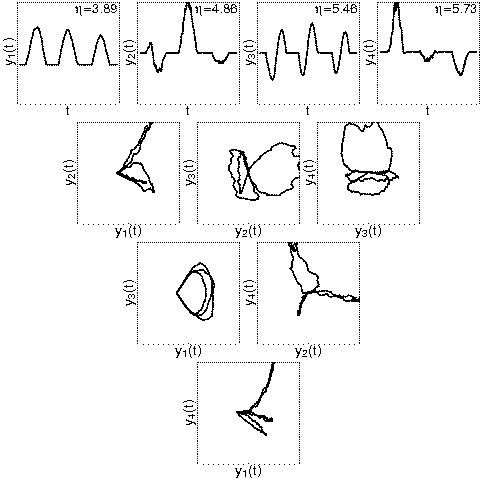
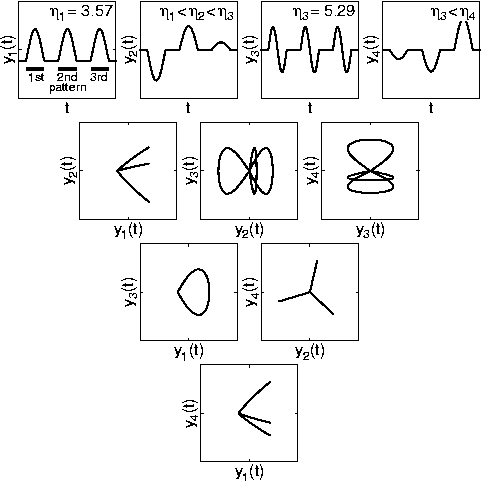
Figure 2: Comparison between experimental and theoretical results. The left (or top) panel shows results from a numerical simulation similar to that illustrated by Animation 2 on the project page Slow Feature Analysis: Unsupervised Learning of Invariances, but including only the first four output signal components. The right (or bottom) panel shows corresponding results as obtained by theoretical considerations. The qualitative agreement is excellent, since the signs of the responses as well as the concrete amplitudes for single patterns are arbitrary.
Black colored reference are the principal ones. Gray colored references are listed for the sake of completeness only. They contain little additional information. .ps-files are optimized for printing; .pdf-files are optimized for viewing at the computer.