Constrained optimization for neural map formation

This project is an attempt to develop a unified theoretical framework for models of neural map formation. The basic architecture consists of an input layer all-to-all connected to an ouput layer. Lateral connections within the layers are fixed while the feed-forward connections are subject to a weight dynamics (growth rule plus normalization rules). The system self-organizes an ordered connectivity between the layers based on induced correlations. Typical examples are retinotopic maps, occular dominance, and orientation columns. But it also includes dynamic link matching as a special form of neural map formation.

The focus of the analysis is on formal aspects. It turns out that the formulation of a system as a constrained optimization problem is particularly convenient and allows us to relate many different models. Growth rules can be derived from objective functions as gradient flows. Normalization rules can be derived from constraints by various methods, e.g. Lagrangian multipliers. Coordinate transformations play an important role in this analysis because they allow us to derive many different weight dynamics and normalization rules from the same optimization problem; see the figure.

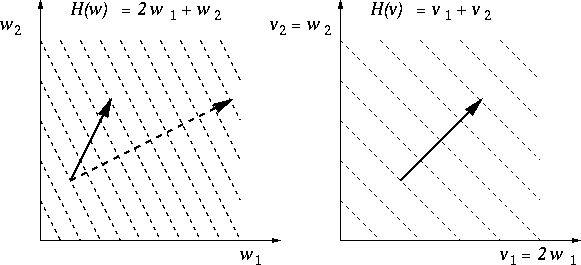
Figure: The effect of a coordinate transformation on a gradient flow. The gradient in the original coordinate system (left, dashed arrow) differs from the gradient evaluated in the new coordinate system (right) and then transformed back (solid arrows) in a characteristic way. This difference induced by a coordinate transformation can be used to derive different dynamics from the same objective function, which is a Lyapunov function for all of the derived dynamics.

Several examples illustrate how objective functions can help in understanding, generating, and comparing different models of neural map formation. For instance, ten different models from the literature are classified within our objective function framework. The techniques used in this analysis may also be useful in investigating other types of neural dynamics.

Relevant Publications:

Black colored reference are the principal ones. Gray colored references are listed for the sake of completeness only. They contain little additional information. .ps-files are optimized for printing; .pdf-files are optimized for viewing at the computer.

5. Wiskott, L. and Sejnowski, T.J. (2001).
   Constrained optimization for neural map formation: A unifying framework for weight growth and normalization.
   In Self-organizing map formation: Foundations of neural computation., eds. Obermayer, K., and Sejnowski, T. J., Cambridge MA, MIT Press, pp. 83-128 (a reprint of WisSej98a).
   (bibtex, abstract.html, paper.pdf, paper.ps.gz)
   
   
4. Wiskott, L. and Sejnowski, T.J. (April 1998).
   Constrained optimization for neural map formation: A unifying framework for weight growth and normalization.
   Neural Computation, 10(3):671-716.
   (bibtex, abstract.html, paper.pdf, paper.ps.gz)
   
   
3. Wiskott, L. and Sejnowski, T.J. (8. October 1997).
   Objective functions for neural map formation.
   Proc. Int'l Conf. on Artificial Neural Networks, ICANN'97, Lausanne, Oct. 8-10, eds. Wulfram Gerstner, Alain Germond, Martin Hasler, and Jean-Daniel Nicoud, number 1327 in series Lecture Notes in Computer Science, publ. Springer-Verlag, Berlin, Heidelberg, pp. 243-248.
   (bibtex, abstract.html)
   
   
2. Wiskott, L. and Sejnowski, T.J. (17. May 1997).
   Objective functions for neural map formation.
   Proc. 4th Joint Symposium on Neural Computation, JSNC'97, Los Angeles, May 17, publ. University of California, San Diego, pp. 242-248.
   (bibtex, abstract.html)
   
   
1. Wiskott, L. and Sejnowski, T.J. (1997).
   Objective functions for neural map formation.
   Institute for Neural Computation Technical Report Series, No. INC-9701. University of California, San Diego, La Jolla, CA 92093, 27 pages.
   (bibtex, abstract.html)